Over 10 years we help companies reach their financial and branding goals. Engitech is a values-driven technology agency dedicated.

Gallery

Contacts

411 University St, Seattle, USA

engitech@oceanthemes.net

+1 -800-456-478-23

Pinterest-p Instagram

Resources

Part 3: Using LAOS to Quantify Long Chain Branching and to Predict Processability

Male Engineer near Alpha Technology instrument

Michele Scacchi

Alpha Technologies

ICYMI – Recap for people who go right to the third blog without reading the first one. 

The presence of long chain branching (LCB) in a polymer has a large impact on his viscoelastic properties and can affect significantly the processability of filled rubber compound: black incorporation time, die swell, extrusion behavior. For instance, the incorporation of long chain branches has been used in EPDM and polyethylene (PE) to enhance shear thinning/flow behavior and, in the case of PEs, to delay the onset of melt fracture toward higher shear rates.

Despite the influence of the molecular architecture of polymer on viscoelastic properties is usually investigated by the linear viscoelastic (LVE) characterization, this approach is not advanced enough to disclose information on complex branching patterns and for fully understanding the processing behavior of elastomers and thermoplastics materials.

FT-Rheology via Large Amplitude Oscillatory Shear (LAOS) is recognized as a very sensitive test method for detecting long chain branching (LCB) or more generally to distinguish different polymer topologies.

How To: Quantify Long Chain Branching

by Using Large Amplitude Oscillatory Shear

As already mentioned in the previous blog about this topic (Read our blog post “FT-Rheology via LAOS Part 1 – Theory” here), the evolution in the shape of the distorted stress waveforms can be related with systematic changes in the internal microstructure of the material or the polymer topologies (linear or branched chain).

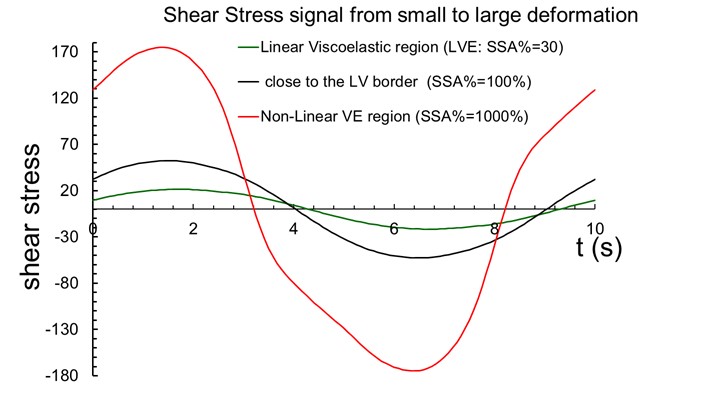
Figure 1: Distortion of the stress signal from small (linear region) to large deformation (non-linear regime)

LAOS responses can be visualized as parametric curves, called Lissajous-Bowditch figures of the oscillating shear stress, t (t) vs. strain γ (t), or t (t) vs. strain-rate, (t).

It was demonstrated that by the Lissajou figure, t (t) vs.  (t), it is possible to distinguish between linear and branched polymers. In fact, secondary loops can only be attributed to polymers characterized by a completely linear macrostructure (could be due to polymer linearity irrespective of average molecular weight and molecular weight distribution). Increasing level of LCB separates the loading part of the stress signal from the unloading part thus, increasing the loop surface and balancing the distortion.

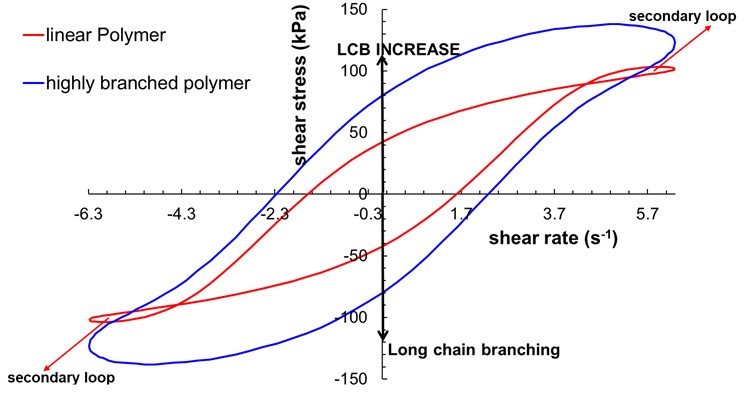
Figure 2: Lissajou figure comparison: linear polymer vs. branched polymer

The mathematical criteria used to determine the analytical condition associated with the onset of the secondary loops was originally proposed by Stadler and Burhin et al. (2008), see Figure 3. Ewoldt and McKinley derived an alternative criterion based on the following condition: G’M < 0. G’M is the minimum-strain modulus used as a measure of non-linear viscoelasticity, and a negative G’M value indicates that the the material is unloading elastic contributions to the instantaneous stress faster than new deformation is being accumulated.

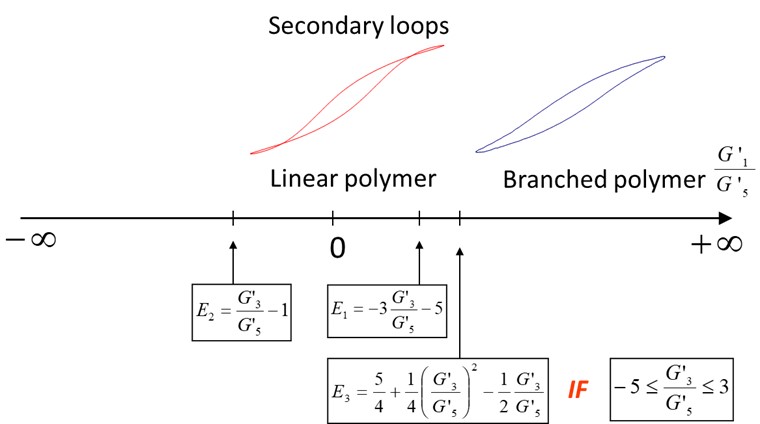
Figure 3: Mathematical condition for secondary loops proposed by University of Louvain

To quantify the level of LCB in the polymers we define a proper criterion and we introduced two LCB indexes: LCB 1 and LCB 2. The first one is the simple ratio between the first and the fifth harmonic component of Gʹ and following this criterion, the greater is this ratio the higher is the level of LCB in the polymer. The second LCB index comes from the theory that I have just shown you and it is mainly used to check the onset of these secondary loops. In fact, only polymers characterized by negative values of this LCB index show secondary loops.

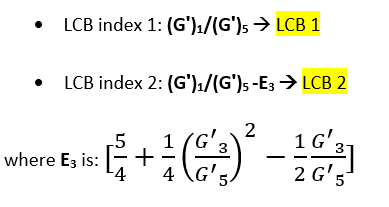
This approach is purely empirical but compared to other rheological test methods it has the big advantage that it depends only on the degree of branching (LCB) and not on the other parameters of the macrostructure, polydispersity, MWD, and molecular weight, Mw, which is both these indexes are insensitive to Mw and MWD.

Other rheologists for the characterization of LCB branched PE and PP grades have proposed two similar LCB indexes, see them below:

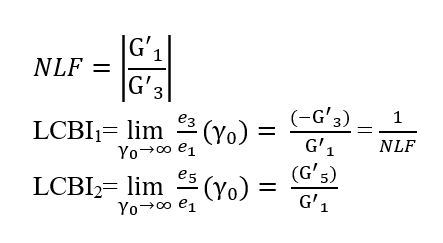
References

  • Roission N 2005 Master thesis. Université Catholique de Louvain (UCL), Faculty of Applied Sciences, Department of mathematical engineering (2004−2005)
  • Ahirwal, D., M., Wilhelm, Filipe, S., et al; Journal of Rheology 58, 635 (2014)
  • Hyun,K., Wilhelm, M., Ewoldt, R., McKinley, G.H., et al; Progress in Polymer Science 36 (2011) 1697–1753
  • Pole, S., Isayev, A.;J Appl Polym Sci. 2021;138
  • Burhin, H.; PMA 2009& 20th SRC 2009
  • Ewoldt, R., McKinley, G.H.;Rheologica Acta · February 2010
  • Ewoldt, R., McKinley, G.H.; J. Rheol. 52(6), 1427-1458

Related Links

More Thought Leadership
♥429